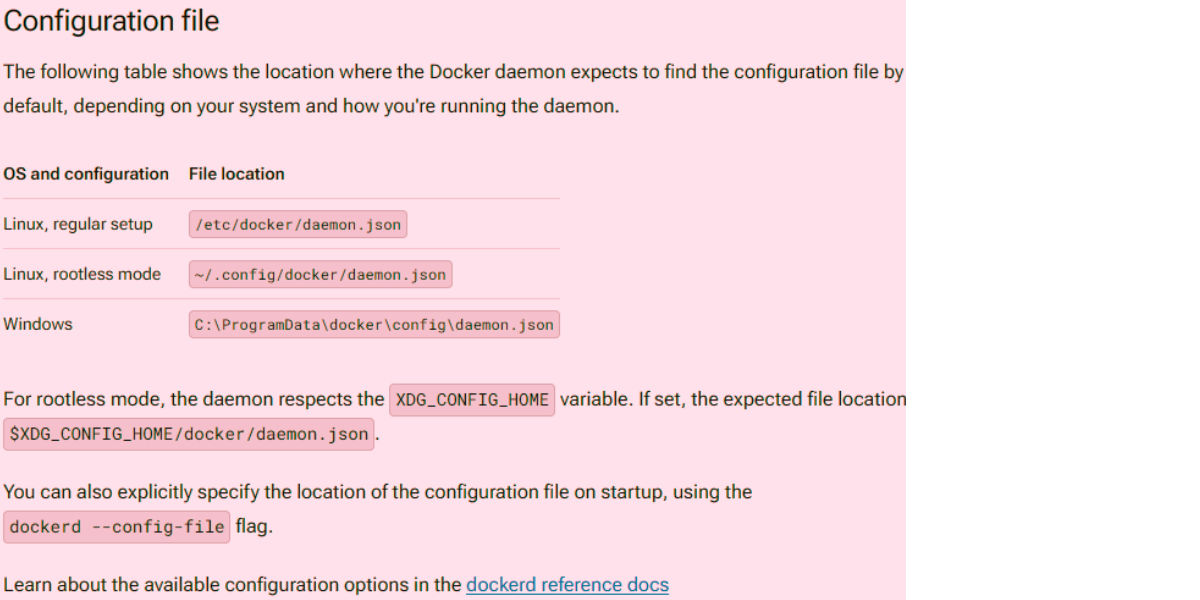
Have you ever wondered how neural networks and machine learning models can be so accurate? It takes more than just the correct algorithm; it also requires the right hyperparameters. Hyperparameters are settings that control the network’s behavior and impact its performance. You can tune these parameters to maximize model performance, but this is often laborious and time-consuming. This blog post will explore some of the most popular hyperparameter optimization techniques available today and how to use them to maximize your model performance.
What Is Hyperparameter Optimization
Hyperparameter optimization tunes a machine-learning model to find the best possible performance. This can be done by manually searching through different combinations of hyperparameters or using an automated search algorithm.
Several methods for hyperparameter optimization include grid search, random search, and Bayesian optimization. Each method has pros and cons, so choosing the right one for your problem is essential.
- Grid search is the simplest method of hyperparameter optimization. It involves trying every combination of hyperparameters until you find the one that gives the best results. This can be very time-consuming, especially if there are many different hyperparameters to optimize.
- Random search is more efficient than grid search since it doesn’t require trying out every combination of hyperparameters. Instead, you randomly select a few combinations to try out. This can still be time-consuming if there are many different hyperparameters to optimize.
- Bayesian optimization is the most sophisticated method of hyperparameter optimization. It uses a Bayesian model approach to determine the relationship between the hyperparameters and the machine learning model’s performance, which makes it efficient.
Understanding the Importance of Hyperparameter Optimization
Hyperparameter optimization is critical for achieving optimal performance from machine learning models. By tuning the hyperparameters of a model, we can control the model’s capacity, complexity, and generalization abilities. In this blog post, we will explore various hyperparameter optimization techniques and how they can be used to maximize model performance.
Manual vs Automatic Hyperparameter Tuning Methods
As machine learning models become more complex, hyperparameter optimization needs increase. There are two main methods for hyperparameter tuning: manual and automatic.
- Manual hyperparameter tuning involves manually selecting the best values for each hyperparameter. This can be a time-consuming process, but it allows the user to understand better the model and how each hyperparameter affects its performance.
- Automatic hyperparameter tuning uses an algorithm to select the best values for each hyperparameter. This can be faster than manual unit g but can sometimes lead to sub-optimal results.
Common Hyperparameters to Optimize in Machine Learning
Several hyperparameters can be tuned to optimize machine learning models. The most common ones are:
- The learning rate controls how quickly the model converges on a solution. A lower learning rate takes longer to train the model but typically results in a more accurate solution.
- The regularization parameter controls how much the model is penalized for fitting too closely to the training data. A higher regularization parameter will make a more straightforward model less likely to overfit the training data.
- The number of hidden layers controls the complexity of the model. More hidden layers allow the model to learn more complex relationships, making it more likely to overfit the training data.
- The number of neurons per hidden layer also controls the model’s complexity. More neurons per hidden layer will allow the model to learn more complex relationships but will again make it more likely to overfit the training data.
Implementing Hyperparameter Optimization in Practice
Regarding hyperparameter optimization, a few different techniques can be used in practice to maximize model performance. The first and most crucial step is to understand the data used to train the model. This includes understanding the data distribution, the essential features, and potential problems that could impact model performance. Once this understanding is gained, the next step is to select a hyperparameter optimization technique that will work well with the data.
A few different techniques can be used, but some more popular ones include grid search, random search, and Bayesian optimization. Each method has advantages and disadvantages, so selecting the one that will work best for the specific data set is essential. After choosing the technique, the next step is implementing it in practice. This includes tuning the model’s hyperparameters and training it on multiple datasets. Finally, it is essential to evaluate the results of the optimized model and compare it to other models to ensure that it is performing as expected.
Evaluating the Effectiveness of Hyperparameter Optimization Techniques
Regarding hyperparameter optimization, a few techniques can be used to find the best possible parameters for a machine-learning model. In this blog post, we will explore two techniques: grid search and random search.
Grid search is an exhaustive search method in which all possible combinations of hyperparameters are tried to find the combination that produces the best performance. This can be very time-consuming, especially if there are many different hyperparameters to tune.
Random search is a more efficient method in which a Random Forest model selects the best hyperparameters from a randomly generated set. It is much faster than grid search and often yields similar results.
We will use the same dataset and machine learning model for both methods to compare their performance. The Iris datasetains 150 observations of iris flowers. This dataset has four features: sepal length, sepal width, petal length, and petal width. We will use all four of these features in our machine-learning model.
The evaluation metric we will use is accuracy, which measures how often our model predicts the correct class label. We will train our models on 80% of the data and test them on 20%. We will repeat this process ten times to obtain a robust accuracy estimate.
Conclusion
In conclusion, hyperparameter optimization is a critical skill for data scientists that enables them to maximize the performance of their models. It involves choosing the correct set of parameters, such as learning rate and regularization strength, to ensure the model fits the data as well as possible. Several techniques are available, ranging from manual tuning to automated algorithms like grid and random search. We explored each method and discussed essential considerations when working with these techniques. With this knowledge, we can confidently work towards optimizing our models’ performances!
FAQS
Q: What is Hyperparameter Optimization?
A: Hyperparameter optimization is the process of tuning the parameters of a model that are not learned during training to improve its performance on unseen data.
Q: Why is Hyperparameter Optimization important?
A: Hyperparameter optimization is essential because it can significantly improve the performance of a model by finding the best combination of parameters for a given dataset and task.
Q: What are some common Hyperparameters to optimize?
A: Some common hyperparameters to optimize include learning rate, number of layers, number of neurons, and regularization strength.
Q: What are the different methods of Hyperparameter Optimization?
A: There are two main methods of hyperparameter optimization: manual tuning and automatic tuning. Manual tuning involves manually adjusting the hyperparameters, while automatic tuning uses algorithms to search for the best combination of hyperparameters.
Q: How can we evaluate the effectiveness of Hyperparameter Optimization?
A: The effectiveness of hyperparameter optimization can be evaluated by comparing the model’s performance before and after optimization, using metrics such as accuracy or F1 score. Additionally, the model can be compared with others with the same architecture but a different set of hyperparameters.