Easy methods to solve LCM and GCF problems with steps

The highest common factor is also known as the greatest common factor (GCF). We can find the HCF of two or more than two numbers. The HCF of two numbers is the greatest number that divides exactly the given number(s), leaving no remainder. Two of the following properties must be considered while solving the mathematics problems regarding HCF. i.e.
- The greatest common factor cannot be zero in any case.
- It is always a positive integer.
- It is always smaller than or equal to the smallest of the given number.
Note: If the HCF of two numbers is equal to 1, then they are called co-prime numbers.
Examples:
- HCF of 12 and 18 is 6.
- HCF of 12 and 20 is 4.
- HCF of 20 and 30 is 10.
Methods To Solve Highest Common Factors:
There are three methods to solve the HCF of two or more numbers
- Factorization Method.
- Prime Factorization Method.
- Division Method.
HCF By Factorization:
Let us consider the following examples to find the HCF by Factorization:
36 AND 48:
Factors of 36 are:
1, 2, 3, 4, 6, 9, 12, 18, 36.
For simplicity and convenience, we can write the factors as
1 x 36, 2 x 18, 3 x 12, 4 x 9, 6 x 6.
Factors of 48 are:
1, 2, 3, 4, 6, 8, 12, 16, 24, and 48
Since in both of the factors, 12 is the highest and 12 is also common so, HCF or GCF of 36 and 48 is 12.
HCF By Prime Factorization:
Here is a complete guide on how to find the HCF of three numbers up to 2 digits by the prime factorization method.
- Find the prime factors of each number.
- Write each number as a product of prime factors
- Identify the common factors of the given numbers
- Multiply all the common factors to get HCF
Example 1:
Now let us suppose that we need to find the HCF of 12 and 8
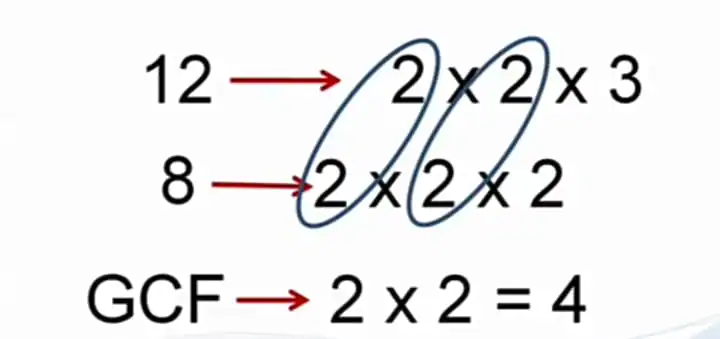
As the figure shows HCF is a product of common multiples so HCF of 12 and 8 is 4.
Example 2:
Suppose you are asked to find the greatest common factor between 24, 32, and 40. The following figure will make the idea clear.
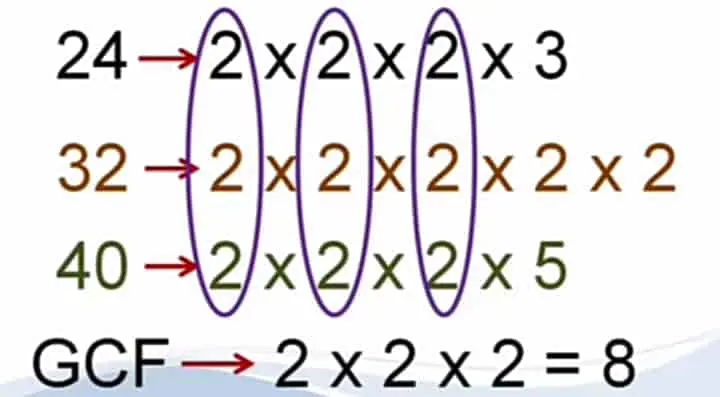
This process is called prime factorization because we are taking the prime factors of the given numbers.
HCF by division method:
This method is more useful for finding HCF. It uses successive divisions to find the HCF. Here we will discuss the complete guide to find HCF by division method.
- Divide the larger number by the smaller number.
- Divide the divisor in step 1 by the remainder in step 1.
- Divide the divisor in step 2 by the remainder in step 2.
- Continue this process till the remainder becomes 0.
- The divisor that eaves the remainder zero is the HCF.
Example:
Suppose we are asked to find the HCF of 120, 160, and 144. First, we need to find the HCF of any of the two numbers. You can find HCF by any method. The following diagram will make the idea clear.
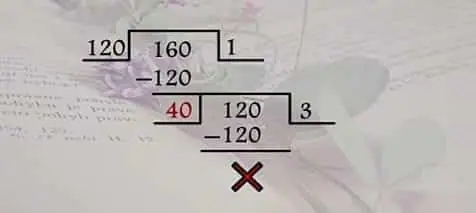
Now we know that 40 is the HCF of 120 and 160.
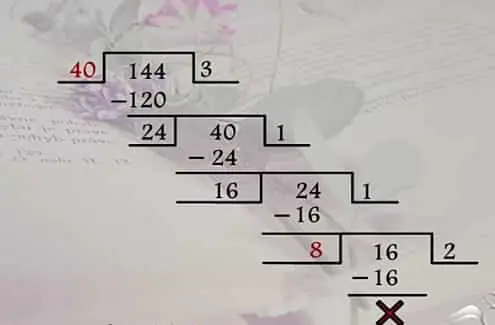
This figure shows that the Highest common factor of 120, 160, and 144 is 8.
Least Common Factors:
LCM is the Acronym for the Least Common Multiple. LCM of two or more numbers is the smallest number that is exactly divisible by the given number.
It is always greater than or equal to the largest of the given numbers.
Examples:
- LCM of 4 and 8 is 8.
- LCM of 6 and 10 is 30.
Methods to solve LCM:
Two methods exist to solve LCM of two or more than two numbers.
- Prime Factorization Method.
- Division Method.
LCM By Prime Factorizaion:
Here is a complete guide to finding LCM by prime factorization:
- Find the prime factors of each of the given numbers.
- Write each number as a product of prime factors.
- Find the product of common factors and the product of non-common prime factors.
- Multiply all the common and the non-common prime factors to get the LCM.
Example:
Suppose we are given 24, 40, 56, and 96. Prime factors of all the given numbers are shown in the figure.

Prime factors of 24 = 2 x 2 x 2 x 3
Prime factors of 40 = 2 x 2 x 2 x 5
Prime factors of 56 = 2 x 2 x 2 x 7
Prime Factors of 96 = 2 x 2 x 2 x 2 x 2 x 3
Product of common prime factors = 2 x 2 x 2 x 3 = 24
Product of non-common prime factors = 2 x 2 x 5 x 7 = 140
LCM = 24 x 140 = 3360
Note: LCM = Product of common prime factors x Product of non-common prime factors.
By Division Method:
Here are the steps to find the LCM of two or more numbers using the division method.
- Write the given number in a row and separate them by putting commas.
- Divide the given number by the smallest prime number, which divides at least one of the given numbers.
- Write the quotients and numbers not divisible by the above prime number in the next row.
- Continue the process of steps two and three until the remainder is a prime number or 1 (one).
- Multiply all the divisors and the remaining prime numbers (if any) to get the LCM.
Example:
Suppose we need to find the LCM of 20, 30, 45, and 60. It can be found in the figure.

LCM = 2 x 2 x 3 x 3 x 5
= 180
So LCM is 180.
HCF and LCM Calculator:
Do you find solving the HCF and LCM problem a bit hectic? Well, you do not have to worry. Developers are coming up with special calculators known as least common multiple calculator or the hcf calculator that help us to calculate the LCM and HCF in less than a second.