Positional Number System and Examples (Updated 2025)
In a positional number system, each symbol represents a different value depending on the position it occupies in a number, and each system has a value that relates to the number directly next to it. The total value of a positional number is the total of the resultant value of all positions. The decimal number system is known as a positional number system because the value of the number depends on the position of the digits. For example, 12345 has a very different value than 54321, although the same digits are used in both numbers. The position in which the digit appears affects the value of that digit.
In a positional number system, the value of each digit is determined by which place it appears in the total number. The lowest place value is the rightmost position, and each successive position to the left has a higher place value. So, the rightmost position represents the “ones” column, the next position represents the “tens” column, the next position represents “hundreds,” and the next position represents the “thousand” and then ten thousand, etc.
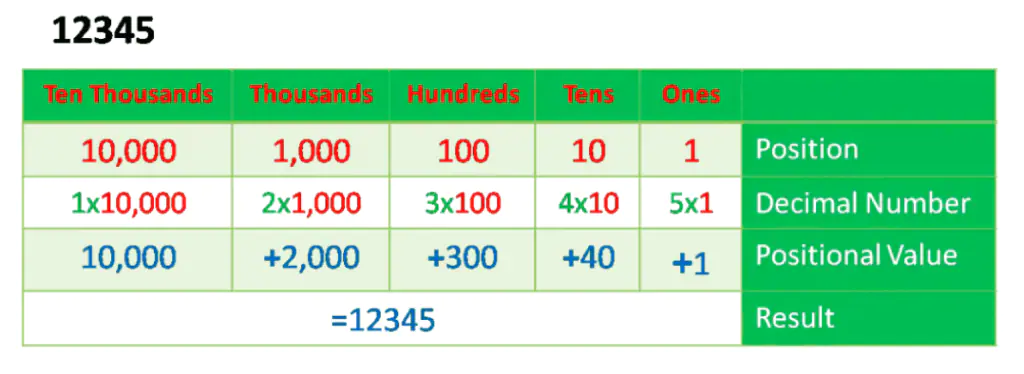
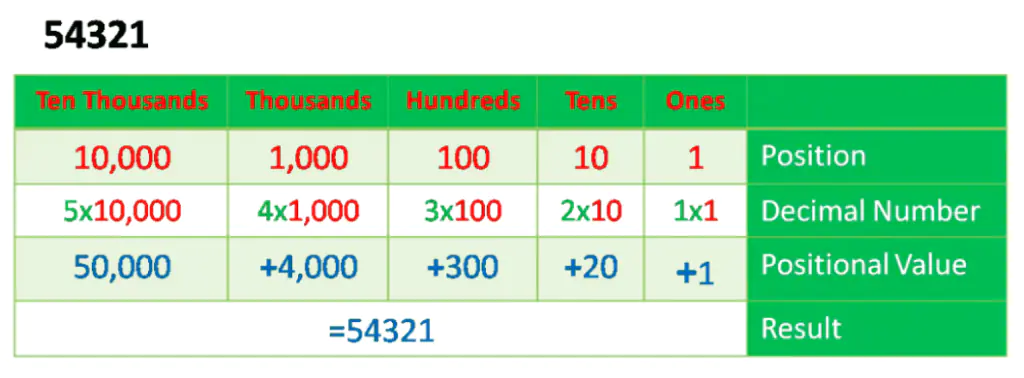
Therefore, the number 54321 represents 5x ten thousand, 4x one thousand, 3x hundred, 2 tens, and 1 x one, whereas the number 12345 represents 1x ten thousand, 2 x one thousand 3 hundred, 4 x tens, and 5 ones. The binary, octal, and hexadecimal are all examples of a Positional Number System. Following is the calculator for conversion between all number systems, and then you can study how to calculate without a calculator.
Number System Converter
Positional vs. Non-Positional Systems
| Aspect | Positional (Decimal) | Non-Positional (Roman Numerals) |
|---|---|---|
| Zero | Supports zero | No zero symbol |
| Arithmetic | Simplifies calculations | Complex and limited |
| Scalability | Handles large numbers | Cumbersome for large values |
Historical Evolution of Number Systems
Babylonians (2000 BCE): A base-60 (sexagesimal) system using wedge-shaped cuneiform symbols, pioneering positional notation for astronomy and trade, with a lasting legacy in time (60 minutes) and geometry (360 degrees).
Mayans (300 BCE): A base-20 (vigesimal) system with dots, bars, and a shell glyph for zero, enabling precise calendrical and astronomical calculations central to their rituals and cosmology.
Indian-Arabic System (500 CE): The decimal (base-10) system with digits 0-9, perfected by Arab scholars, revolutionized global mathematics through positional notation and zero’s dual role as placeholder and numeral.
Decimal Positional Notation
The decimal positional notation system works as described in the table in the figure below. To use the positional number system, match a given number to its positional value. The arrow at the left shows that the table can be expanded according to position and can be calculated.
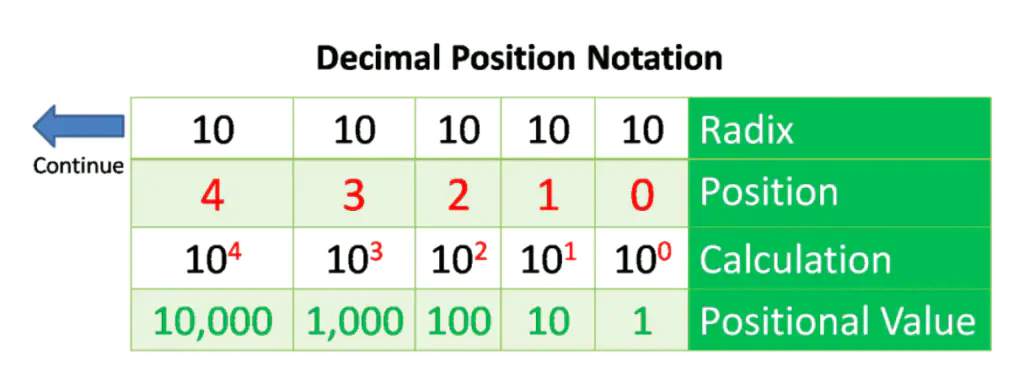
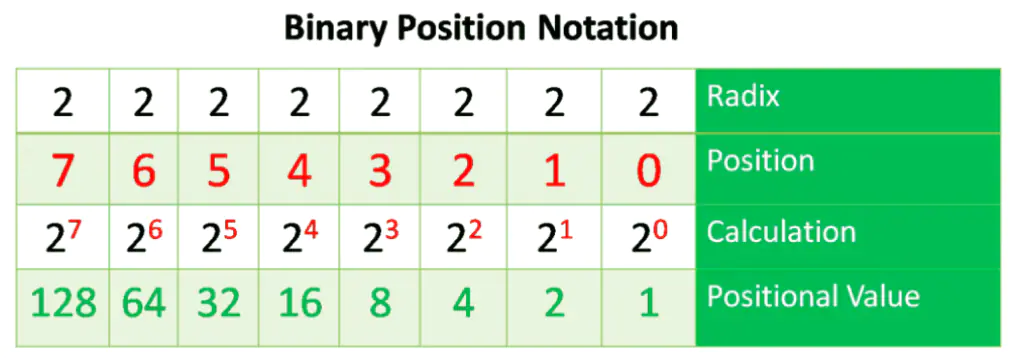
Radix
The Term Radix describes the number of digits utilized in the positional number system to identify the system’s base. The decimal notation system is based on 10, so the radix is 10.
Position in
It shows the position of the decimal number. The position starts from the right and moves to the left. So 0 is the 1st position 1 is the 2nd position, 2 is the 3rd position, and so on. The numbers also represent the exponential value that will be used to calculate the positional value of the 4th row.
Calculate
The third row calculates the positional value by taking the radix and raising it to the power of its position. Importantly, n0 is always = 1.
Position Value
The first row shows the number base or radix. From left to right, the values listed represent units of thousands, hundreds, tens, and ones.
Example – 12345 and 54321
Binary Positional Notation
The binary positional notation also operates similarly to the decimal number system, as shown in the figure below. It also has a Radix, Position, which is from right to left; Calculation and positional value as described for decimal. The Radix for Binary is 2. The example is also shown below
Examples
Converting Between Decimal and Binary
Converting binary to decimal (base-2 to base-10) numbers and back is an essential concept for understanding the binary numbering system. Binary number systems form the basis for all computers, digital systems, and programming languages, and they are also essential for comprehending IP address and IP address subnetting.
Binary to Decimal Conversion
To understand IP addressing and subnetting, the network technician must understand how to convert from binary to decimal. There are several ways to convert from binary to decimal. Here, we will realize conversion from binary to decimal and then from decimal to binary.
Binary to Decimal Using Positional Notation
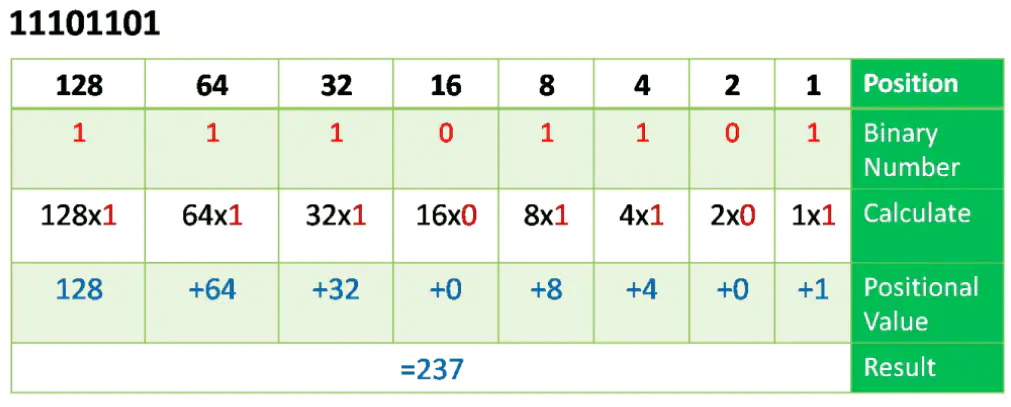
Positional notation is one of the most used methods for converting binary and decimal, so if we have a binary number 110001102 and want to convert this number to decimal base 10 system using the positional system notation.
The figure below illustrates the conversion of the binary to decimal. Write down the positional value from right to left and right down the binary number in the next row below the positional values. Next, multiply the binary numbers in the second row with their corresponding positional value in the first row and add them up to get the decimal number 199.

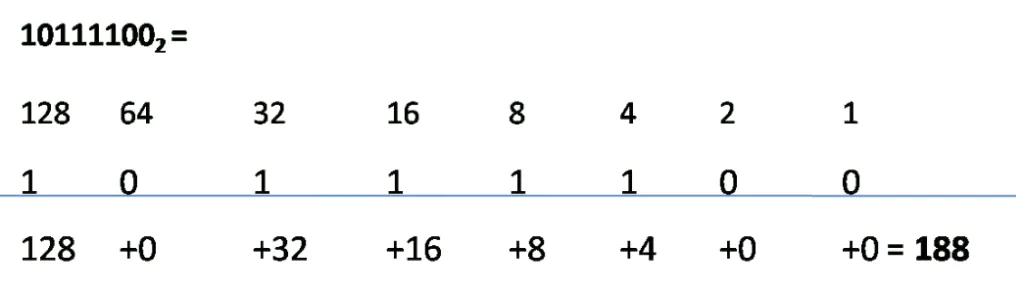
The positional value doubles from right to left. For example, from right to left, the first positional value is 1, the next position value is 2, double 1 (the first position value), and the third place value is 4, double the second position value. We can write positional values using this method according to the binary digits.
The following binary value is 10111100. So, write the positional value according to the number of digits in the binary value. Then, write the binary numbers below the positional values and map them up. If the digit is a 1, write its corresponding positional value below the line, under the digit. If the digit is a 0, write a 0 below the line, under the digit, and add up the numbers written below the line. This is the decimal equivalent of the binary number. See figure the figure below.
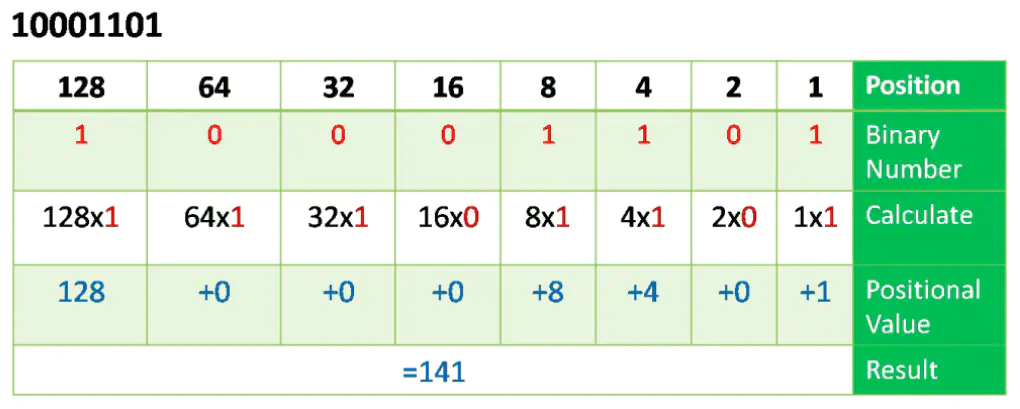
Now that we understand the basic conversion from binary to decimal, we can try to convert a binary IPv4 address to its dotted-decimal equal. First, divide 32 bits of the IPv4 address into four 8-bit octets. Then, calculate the binary positional value of the first octet binary number and all others.
For example, consider that 11110110.10111111.11101011.11011011 is the binary IPv4 address. As shown in the Figure below, you must convert the binary address to decimal, starting from the first octet. Enter the 8-bit binary number under the positional value of row 1 and then calculate to produce the decimal number for the first octet of the dotted decimal notation. Next, convert the remaining octets. Write down the full IP address using dotted decimal notation.

Decimal to Binary Conversion
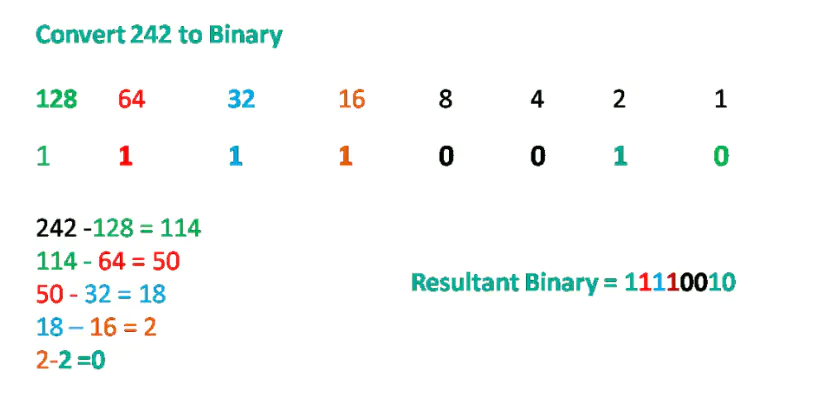
Decimal to binary conversion is also essential to understand; we can convert a dotted decimal IPv4 address to binary. We can also use a positional value table to convert from decimal to binary. The figure below illustrates the decimal to the binary conversion process. For example, we want to convert Figure 246 into binary. The steps for converting from decimal to binary are the following:
Step-1
Write down the positional value from left to right, as shown in the figure below. If the decimal number (242 in our case) is equal to or greater than the most significant bit (128), add a binary 1 below the 128 positional value and subtract 128 from the decimal number (242 -128 =114 in our case). If not, enter binary 0 below the 128 positional value.
Step-2
Compare if the remainder (114) equals or exceeds the next most significant bit (64). If yes, add a binary 1 below the 64 positional value and subtract the positional value 64 from the decimal number (114 -64 =50 in our case). If no, then enter binary 0 below the 64 positional value.
Step-3
Compare if the remainder (50) equals or exceeds the next most significant bit (32). If yes, add a binary 1 below the 32 positional value and subtract the positional value 32 from the decimal number (50 -32 =18 in our case). If no, then enter binary 0 below the 64 positional value.
Step-4
Compare if the remainder (18) equals or exceeds the next most significant bit (16). If yes, add a binary 1 below the 16 positional value and subtract the positional value 16 from the decimal number (18 -16 =2 in our case). If no, then enter binary 0 below the 16 positional value.
Step-5
Compare the reminder (2) with the following -most significant bit, you can see that the remainder is less than the considerable value (80), so add a binary 0 in the 8 positional value and step forward to the next positional value, which is (4), the remainder is also less than this positional value, so, add 0 below this position value and step forward to next value. The next value is positional value is (2), So, Subtract the reminder 2 from the positional value (2-2=0), put the 0 in the last position.
Where Are Positional Number Systems Used?
Binary in Computers:
- Transistors use binary (0=off, 1=on) to perform calculations.
- Example: RGB colors like
#FF0000(pure red) use binary values (0-255) for intensity.
Hexadecimal in Web Design:
- Hex codes simplify color selection (e.g.,
#1A3FBC= blue shade). - Memory addresses in programming (e.g.,
0x1A3F).
Base-60 in Timekeeping:
- Babylonian legacy: 60 seconds/minute, 60 minutes/hour.
FAQs
-
A positional system assigns value to digits based on their position, unlike non-positional systems like Roman numerals.